Image:Lemniscates5.png

[edit] Summary

[edit] Long description

Few lemniscates of Mandelbrot set^[1]. They are boundaries of Level Sets of escape time ( LSM/M ^[2]).

They are in parameter plane (c-plane, complex plane ).

Definition :

where

is Escape Radius, bailout value, radius of circle which is used to measure if orbit of 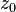is bounded; it is integer number

are complex numbers (points of 2-D planes )

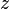is point of dynamical plane ( z-plane)

is point of parameter plane ( c-plane)

critical point of

One can compute first few iterations :

and so on .

Then :

...

is a circle,

is an Cassini oval,

is a pear curve^[3].

These curves tend to boundary of Mandelbrot set as n goes to infinity.

If ER<2 they are inside Mandelbrot set^[4].

If ER=2 curves meet together ( have common point) c=-2. Thus they can't be equipotential lines.

If ER>=2 they are outside of Mandelbrot set. They can also be drawn using Level Curves Method.

If ER>>2 they aproximate equipotential lines ( level curves of real potential , see CPM/M ).

[edit] Maxima source code

/* based on the code by Jaime Villate */
load(implicit_plot); /* package by Andrej Vodopivec */
c: x+%i*y;
ER:2; /* Escape Radius = bailout value it should be >=2 */
f[n](c) := if n=1 then c else (f[n-1](c)^2 + c);
ip_grid:[100,100];  /* sets the grid for the first sampling in implicit plots. Default value: [50, 50] */
ip_grid_in:[15,15]; /* sets the grid for the second sampling in implicit plots. Default value: [5, 5] */
my_preamble: "set zeroaxis; set title 'Boundaries of level sets of escape time of Mandelbrot set'; set xlabel 'Re(c)';  set ylabel 'Im(c)'";
implicit_plot(makelist(abs(ev(f[n](c)))=ER,n,1,6), [x,-2.5,2.5],[y,-2.5,2.5],[gnuplot_preamble, my_preamble],
[gnuplot_term,"png   size  1000,1000"],[gnuplot_out_file, "lemniscates6.png"]);

For curves 1-5 it works, but for curve number 6 this program fails( also Mathemathica program^[5]), because of floating point error.

One have to change the method of computing lemniscates . Here is the code and explanation by Andrej Vodopivec" "You can trick implicit_plot to do computations in higher precision. Implicit_draw will draw the boundary of the region where the function has negative value. You can define a function f6 which computes the sign of f[6] using bigfloats and then plot f6."

/* based on the code by Jaime Villate and Andrej Vodopivec*/
c: x+%i*y;
ER:2;
f[n](c) := if n=1 then c else (f[n-1](c)^2 + c);
F(x,y):=block([x:bfloat(x), y:bfloat(y)],if abs((f[6](c)))>ER then 1 else -1); 
fpprec:32;
load(implicit_plot); /* package by Andrej Vodopivec */ 
ip_grid:[100,100];
ip_grid_in:[15,15];
implicit_plot(append(makelist(abs(ev(f[n](c)))=ER,n,1,5), ['(F(6,x,y))]),[x,-2.5,2.5],[y,-2.5,2.5]);

[edit] Rerferences

1. ↑ lemniscates at Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo
2. ↑ LSM/M
3. ↑ Weisstein, Eric W. "Pear Curve." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PearCurve.html
4. ↑ Polynomial_lemniscate
5. ↑ | Weisstein, Eric W. "Mandelbrot Set Lemniscate." From MathWorld--A Wolfram Web Resource.

[edit] Licensing:

I, the copyright holder of this work, hereby publish it under the following licenses: Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation license, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled "GNU Free Documentation license". Aragonés | العربية | Asturianu | Български | বাংলা | ইমার ঠার/বিষ্ণুপ্রিয়া মণিপুরী | Brezhoneg | Bosanski | Català | Cebuano | Česky | Dansk | Deutsch | Ελληνικά | English | Esperanto | Español | Eesti | Euskara | فارسی | Suomi | Français | Gaeilge | Galego | עברית | Hrvatski | Magyar | Bahasa Indonesia | Ido | Íslenska | Italiano | 日本語 | ქართული | ភាសាខ្មែរ | 한국어 | Kurdî / كوردی | Latina | Lëtzebuergesch | Lietuvių | Bahasa Melayu | Nnapulitano | Nederlands | ‪Norsk (nynorsk)‬ | ‪Norsk (bokmål)‬ | Occitan | Polski | Português | Română | Русский | Slovenčina | Slovenščina | Shqip | Српски / Srpski | Svenska | తెలుగు | ไทย | Türkçe | Українська | اردو | Tiếng Việt | Volapük | Yorùbá | ‪中文(中国大陆)‬ | ‪中文(台灣)‬ | +/- This file is licensed under the Creative Commons Attribution ShareAlike license versions 3.0, 2.5, 2.0, and 1.0 Български | Català | Česky | Dansk | Deutsch | Ελληνικά | English | Español | Euskara | Estremeñu | Français | עברית | Italiano | 日本語 | 한국어 | Lietuvių | Nederlands | ‪Norsk (bokmål)‬  | Occitan | Polski | Piemontèis | Português | Русский | 中文 | +/- You may select the license of your choice.

• Polynomial lemniscate